重要声明:本文章仅仅代表了作者个人对此观点的理解和表述。读者请查阅时持自己的意见进行讨论。
本文的讲解及代码部分都是针对Java语言,可能对其它语言并不适用,但介于这部分内容较底层,因此可酌情参考。
一、认识二进制
二进制,是计算技术中广泛采用的一种数制,由德国数理哲学大师莱布尼茨于1679年发明。二进制数据是用0和1两个数码来表示的数。它的基数为2,进位规则是“逢二进一”,借位规则是“借一当二”。当前的计算机系统使用的基本上是二进制系统,数据在计算机中主要是以补码的形式存储的。计算机中的二进制则是一个非常微小的开关,用“开”来表示1,“关”来表示0。摘自百度百科。
二、位 - bit
计算机能保存的最小数据单位:位(bit),常常也叫:比特。一个位保存的数据,要么是0,要么是1。
由于一个位的数据存储量太少,因此大多数情况下都是几个位组成多个来使用。下面就是常见的基本类型定义:
- byte: 由8个位组成。
- short: 由16个位组成
- char: 由16个位组成
- int: 由32个位组成
- float: 由32个位组成
- long: 由64个位组成
- double: 由64个位组成
同时 byte、short、int、long (即整数)在保存数据时,高位表示符号位,用1表示负数,用0表示正数。所谓最高位,就是从左数的第一位。当表示负数时,实际值要对所有位取反然后加1。比如:
使用byte作为案例,因为只有8位,篇幅占用少。
00000010: 表示整数 2
11111110: 表示整数 -2。
取值过程:
第一步:观察最高位是1,因此取反,得:00000001
第二步:取反后加1,得:00000010
得出结果:2,取负得:-2。
为了直观观察,常常每4位写一个空格:
0000 0010 = 2
1111 1110 = -2
1、二进制转十进制
二进制十分不便于阅读,而十进制是从小就接触到的。所以,将二进制数据转换为十进制经常用到各种场合。甚至大多数情况下,都是将数据转换为十进制进行使用。
先从简单开始,首先来说说十进制:
十进制的基数是:0, 1, 2, 3, 4, 5, 6, 7, 8, 9
当我们数数时,数到第十时,由于基数里没有一个数字可以直接表示十这个数,所以产生了进位,到第九时,若要继续数下去,那么就进一位,从而变成:10。使用了基数 1 和基数 0 组合起来,形成 10。
同样的道理,二进制的基数是:0, 1
当我们数数时,数到二时,由于基数里没有一个数可以直接表示二这个数,所以也要进位。那么进一位后就形成了:10。
那么,不妨来多罗列几个数字,形成直观的感受:
二进制 十进制
1 == 1
10 == 2
11 == 3
100 == 4
101 == 5
110 == 6
111 == 7
1000 == 8
1001 == 9
1010 == 10
1011 == 11
1100 == 12
1101 == 13
1110 == 14
1111 == 15
数字简单的话,可以通过一个一个的数数,直接反应出结果,但如果有一个很长的二进制数,用数数的方法显然也没法快速完成了,我们必须使用一套计算方法来完成这个工作了,先来看一张图:
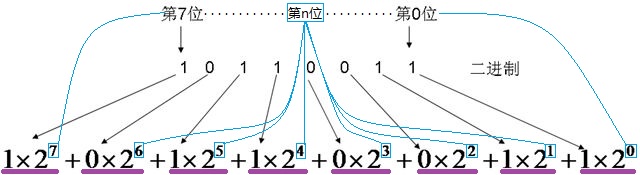
按照图上的公式,计算出接过来,就可以得到十进制的结果了。
2、十进制转二进制
有了上面一小节的知识后,就很容易理解各进制间的关系了。那么从十进制转换为二进制又该如何转换呢,这节知识应该在高中时就有所学习了:
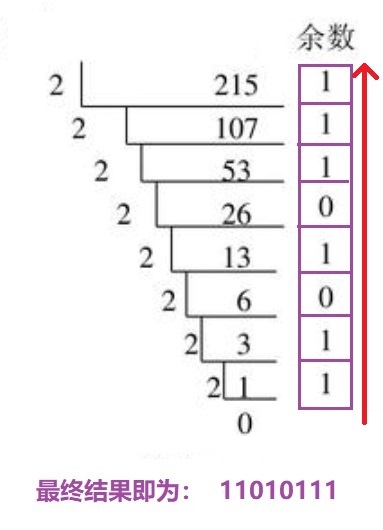
使用图上的计算方式,每次除以2,然后取余数,最终商为0时停止计算,上图中:215的二进制表示为:11010111。
三、字节 - byte
一个字节由8个位组成,因此他能容纳的整数范围也就被框定在了:[-128, 127] 之间,为什么在这个范围之间?不妨看看下面的推理过程:
一个byte占8位,而最高位0表示正数,1表示负数。
因此不难得出最小值:1000 0000, 最大值:0111 1111
最小值:1000 0000。将实际值计算出来:
1、最高位是1,为负数,先取反得:0111 1111;
2、再加1得:1000 0000;
3、使用上面的公式计算:1x(2^7)+0x(2^6)+...+0x(2^0) = 128
4、由于最高位是1,表示负数,得到最终结果:-128
最大值:0111 1111。将实际值计算出来:
1、直接使用公式计算:1x(2^6)+1x(2^5)+...+1x(2^0) = 127
2、由于最高位是0,直接确定最终结果:127
所以为什么byte的容量只能在: [-128, 127] 子间,这就是原因所在了。
阅读了上面的推导过程,细心的朋友不难发现,当最大值再进行加1操作过后,其结果在二进制层面上立刻就变成了最小值,再反应到十进制输出时,就直接成了: 127 + 1 = -128 这样的非常规结果了。主要原因就在于,byte最大值就是127,而再进行加1,最高位就变成了1,立刻就发生了质的变法,从正数变成了负数,还不小心成了byte里最小的负数。(实际上127+1赋值给byte是会报错的,但如果你把128通过强制转换成byte,则会出现此问题。)
四、短整型 - short
在实际编程过程中,并不经常用到它,可能比较重要的一个原因就是它能容纳的数据不大。但即便是不大,它也比字节(byte)多占用1倍的空间。短整型占用了 16 个位,也就相当于 2 个字节的容量。因此不难得到它的最大最小范围:1000 0000 0000 0000 ~ 0111 1111 1111 1111,写出十进制值则是:
-32768 ~ 32767。计算过程可以按照上一节的方式计算出来。
五、整型 - int
整型是实际编程过程中最常用的基本类型之一,它由 32 个位组成,显然能存储的数字就更大。它的取值范围是:-2147483648 ~ 2147483647 。 这个容量对于大多数场景来说,都已经适用了。
六、长整型 - long
长整型的数据存储容量又是整型的2倍,它由 64 个位组成。取值范围是:-9223372036854775808 ~ 9223372036854775807。
七、浮点
浮点类型的数据可以支持小数点在内,这样一来就为程序里支持小数点提供了解决方案。不过它不是精确表示的,意味着在有时候得到的结果可能并不是一个精确的数字。java针对浮点类型数在内存里的保存方式是遵循了 IEEE 754标准 的。因此,要了解浮点数是如何保存的,只需要了解这个标准是如何制定的就知道了。同时下面也会对其做详细的介绍。
1、十进制小数与二进制的互换
在开始了解浮点数前,有必要先了解一下十进制小数是怎么和二进制进行转换的。对于十进制小数的转换为二进制,需要分为两部分处理,整数部分和小数部分。
1)、十进制->二进制
例如我将:24.13 转换为二进制。
整数部分
整数部分也就是小数点左边部分,是:24。可以直接使用上边几节的知识将其进行转化为二进制,为节省篇幅,此处直接得出结果:11000。
小数部分
小数部分也就是小数点右边部分,是:0.13。我们知道,整数部分转换为二进制是使用除法取余,最终倒序取结果的方式。而针对小数部分,就不是这样计算的了,甚至计算方式相反,要进行乘法运算了。小数部分转化二进制,常常采用乘2取整的方法。就是将小数部分乘以2,得到的结果取其整数部分。例如将0.13转化为二进制:
// 只对小数部分乘2取整。
0.13 × 2 = 0.26 -> 取整数部分得:0 ,下次计算只使用小数部分:0.26
0.26 × 2 = 0.52 -> 取整数部分得:0 ,下次计算只使用小数部分:0.52
0.52 × 2 = 1.04 -> 取整数部分得:1 ,下次计算只使用小数部分:0.04
0.04 × 2 = 0.08 -> 取整数部分得:0 ,下次计算只使用小数部分:0.08
0.08 × 2 = 0.16 -> 取整数部分得:0 ,下次计算只使用小数部分:0.16
0.16 × 2 = 0.32 -> 取整数部分得:0 ,下次计算只使用小数部分:0.32
0.32 × 2 = 0.64 -> 取整数部分得:0 ,下次计算只使用小数部分:0.64
0.64 × 2 = 1.28 -> 取整数部分得:1 ,下次计算只使用小数部分:0.28
0.28 × 2 = 0.56 -> 取整数部分得:0 ,下次计算只使用小数部分:0.56
0.56 × 2 = 1.12 -> 取整数部分得:1 ,下次计算只使用小数部分:0.12
0.12 × 2 = 0.24 -> 取整数部分得:0 ,下次计算只使用小数部分:0.24
0.24 × 2 = 0.48 -> 取整数部分得:0 ,下次计算只使用小数部分:0.48
0.48 × 2 = 0.96 -> 取整数部分得:0 ,下次计算只使用小数部分:0.96
0.96 × 2 = 1.92 -> 取整数部分得:1 ,下次计算只使用小数部分:0.92
0.92 × 2 = 1.84 -> 取整数部分得:1 ,下次计算只使用小数部分:0.84
0.84 × 2 = 1.68 -> 取整数部分得:1 ,下次计算只使用小数部分:0.68
0.68 × 2 = 1.36 -> 取整数部分得:1 ,下次计算只使用小数部分:0.36
0.36 × 2 = 0.72 -> 取整数部分得:0 ,下次计算只使用小数部分:0.72
0.72 × 2 = 1.44 -> 取整数部分得:1 ,下次计算只使用小数部分:0.44
0.44 × 2 = 0.88 -> 取整数部分得:0 ,下次计算只使用小数部分:0.88
0.88 × 2 = 1.76 -> 取整数部分得:1 ,下次计算只使用小数部分:0.76
0.76 × 2 = 1.52 -> 取整数部分得:1 ,下次计算只使用小数部分:0.52
0.52 × 2 = ....... 发现又一次出现0.52,这和第4行的产生了重复,继续乘下去也会一直这样下去,这里就产生了二进制上的循环。
那么此时,可得到小数(为了显示清晰,在循环部分我使用空格分开):
0.13 转化为二进制为:00 10000101000111101011 10000101000111101011....循环
拿到了小数部分的二进制结果,再加上整数部分的二进制结果就得到了:
24.13 = 11000.00 10000101000111101011 10000101000111101011....循环
2)、二进制->十进制
在上边的讲解 位(bit) 的小节阐述了如何将二进制数据直接转化为十进制,你可以使用同样的方法将带小数的二进制数据代入公式进行计算。就拿上边得到的结果来进行运算
整数部分
整数部分十分简单,可直接套入公式:
11000 = 1×(2^4)+1×(2^3)+0×(2^2)+0×(2^1)+0×(2^0) = 24
小数部分
或许你会对小数部分感到迷惑,实际上知道真相的你眼泪会掉下来。在上面整数计算过程中,其指数部分由高到低分别降低: 4-3-2-1-0,而小数部分,可以继续降低,然后使用同样的方法:
00 10000101000111101011 10000101000111101011....循环 = 0×(2^-1)+0×(2^-2)+1×(2^-3)+0×(2^-4)+0×(2^-5)+0×(2^-6)+0×(2^-7)+1×(2^-8)++0×(2^-9)+1×(2^-10)+0×(2^-11).... ≈0.13
最终整数部分加上小数部分的结果,即可顺利得到最终结果:
11000.00 10000101000111101011....循环 = 1×(2^4)+1×(2^3)+0×(2^2)+0×(2^1)+0×(2^0)+0×(2^-1)+0×(2^-2)+1×(2^-3)+0×(2^-4)+0×(2^-5)+0×(2^-6)+0×(2^-7)+1×(2^-8)++0×(2^-9)+1×(2^-10)+0×(2^-11).... ≈ 24.13
从这样一个计算过程,也不难发现,在处理小数的保存时,精度问题也逐渐的暴露了出来。
2、单精度浮点 - float
单精度浮点数占用32个位空间,它和整型(int)占用相同数量的空间。但它的取值范围计算方式和整型(int)的取值范围计算方式大不一样。由于浮点数在计算机中的保存方式和整型的保存方式不一样,从而导致了它们的取值范围不一样。java对浮点数的保存方式遵循了 IEEE 754标准 标准。在了解单精度浮点的范围之前,不妨先来一窥 IEEE 754标准 的真面目。
IEEE 754 标准
IEEE二进制浮点数算术标准(IEEE 754)是20世纪80年代以来最广泛使用的浮点数运算标准,为许多CPU与浮点运算器所采用。这个标准定义了表示浮点数的格式(包括负零-0)与反常值(denormal number)),一些特殊数值(无穷(Inf)与非数值(NaN)),以及这些数值的“浮点数运算符”;它也指明了四种数值舍入规则和五种例外状况(包括例外发生的时机与处理方式)。了解更多。
标准什么的看起来可能会比较难以理解,不如先看一下这张图来入个门吧:

符号位
只占用第一个位,这个很容易理解,它的作用就是确定这个数是负数还是正数。这个整数类型首位符号位是一个意思。
指数部分
占用了接下来的8个位,这部分保存了指数部分的值,需先将十进制小数转化为二进制小数,然后转化成二进制科学计数法的小数,然后将其指数部分加上偏移(127)再保存到指数部分。例如:
比如我们将小数 13.625 的指数部分要保存的值求出来:
第一步 - 先化十进制小数为二进制,根据上面的知识,很容易得到:1101.101
第二步 - 化二进制结果为科学计数法。
要注意这个过程有个规定:化为科学计数法时必须要保证小数点左边只有一个数并且这个数只能是1。
因此这里我们只需要将 1101.101 向右移动(即小数点向左)3个位置,就可得到结果:1.101101 × 2^3
第三步 - 将指数实际值加上偏移127。得:3 + 127 = 130
第四步 - 计算 130 的二进制结果,按照上面的知识即可技术得到结果:1000 0010
最终,我们拿到小数 13.625 的指数部分要保存到计算机的结果:1000 0010
底数部分
这部分占用了剩下的所有23个位。它负责保存底数部分,就比如上面的推导过程中,二进制科学计数法时,其数据的底数就是 1.101101,而规定了小数点左边只能是1,因此保存时只保存小数点右边部分 101101,这个数据量还没有达到 23 个,可在后面补0直到23个。例如:
接上一部分推导。我们已经拿到了 13.625 的二进制科学计数表示结果:1.101101 × 2^3
第一步 - 取底数:1.101101
第二部 - 左边始终为1,只需保存小数点右边部分:101101
第三步 - 不足23位,补0。
最终得到底数部分要保存的值:101101 000000 000000 00000
最后,再结合符号位、指数部分、 底数部分,将小数 13.625 保存到计算机的完整结果:
小数:13.625
入计算机:0 10000010 10110100000000000000000
3、单精度浮点 - float - 取值范围
那么有了这些了解之后,就很容易得出单精度浮点数的最小值和最大值了 1 11111111 11111111111111111111111 ~ 0 11111111 11111111111111111111111。现在不妨来计算一下它们的十进制值:
先计算最小值:1 11111111 11111111111111111111111
第一步 - 确定正负。观察首位是1,表示负数。
第二步 - 计算指数。指数位: 11111111
将二进制数:11111111 转化为十进制得:255
由于存入时的指数是加了偏移127的,因此取出时要减去,得: 255-127 = 128
第三步 - 计算底数。底数为:11111111111111111111111
由于底数存储是使用的小数点右边部分,因此取出是要加上原本左边的[1.]。
得到结果:1.11111111111111111111111
第四步 - 拼接为科学二进制计数法。
将底数和指数结合,得:1.11111111111111111111111 × 2^(128)
第五步 - 转为二进制常规计数法。
得到:1 11111111111111111111111 00...00 (除第一个1外,有23个1。共104个0)
第六步 - 将此二进制数计算为十进制。
1×(2^127) + 1×(2^126) + ... + 1×(2^104) + 0×(2^103) + ... + 0×(2^0)
= 340282346638528859811704183484516925440
第七步 - 取负值。应为原始二进制数据首位是1,因此取负值。
最终得到 float 最小值为:-340282346638528859811704183484516925440
针对最大值的计算,其实计算方式相同。只是首位正负不同而已。
那么最终可得到float的十进制取值范围:
-340282346638528859811704183484516925440 ~ 340282346638528859811704183484516925440
4、双精度浮点 - double
双精度浮点占用了 64 个位,它与单精度浮点数在数据存入计算机时是使用相同的原理。只是数据量大小的区别。区别如下:
| 区域 | 单精度(float) | 双精度(double) |
|---|---|---|
| 符号位 | 占1位 | 占1位 |
| 指数位 | 占8位 | 占11位 |
| 指数位偏移值 | 127 | 1023 |
| 底数位 | 23位 | 52位 |
八、字符 - char
字符(char)占用了16个位,它在内存中实际上保存的是字符对应的ASCII码值,而该值就是一个整型数据,因此其存储逻辑和整型数据是一致的,只是在读取时,会根据ASCII码表进行对应转换。常见的ASCII字符码值如下:
| 字符 | 码值 | 字符 | 码值 | 字符 | 码值 |
|---|---|---|---|---|---|
| 空 | 0 | \t | 9 | \n | 10 |
| \r | 13 | 空格 | 32 | ||
| ! | 33 | " | 34 | # | 35 |
| $ | 36 | % | 37 | & | 38 |
| ' | 39 | ( | 40 | ) | 41 |
| * | 42 | + | 43 | , | 44 |
| - | 45 | . | 46 | / | 47 |
| 0 | 48 | 1 | 49 | 2 | 50 |
| 3 | 51 | 4 | 52 | 5 | 53 |
| 6 | 54 | 7 | 55 | 8 | 56 |
| 9 | 57 | : | 58 | ; | 59 |
| < | 60 | = | 61 | > | 62 |
| ? | 63 | @ | 64 | A | 65 |
| B | 66 | C | 67 | D | 68 |
| E | 69 | F | 70 | G | 71 |
| H | 72 | I | 73 | J | 74 |
| K | 75 | L | 76 | M | 77 |
| N | 78 | O | 79 | P | 80 |
| Q | 81 | R | 82 | S | 83 |
| T | 84 | U | 85 | V | 86 |
| W | 87 | X | 88 | Y | 89 |
| Z | 90 | [ | 91 | |92 | |
| ] | 93 | ^ | 94 | _ | 95 |
| ` | 96 | a | 97 | b | 98 |
| c | 99 | d | 100 | e | 101 |
| f | 102 | g | 103 | h | 104 |
| i | 105 | j | 106 | k | 107 |
| l | 108 | m | 109 | n | 110 |
| o | 111 | p | 112 | q | 113 |
| r | 114 | s | 115 | t | 116 |
| u | 117 | v | 118 | w | 119 |
| x | 120 | y | 121 | z | 122 |
| { | 123 | | | 124 | } | 125 |
| ~ | 126 |
你可以使用这段代码把所有字符打印出来:
for (char i = 0; i < Character.MAX_VALUE; i++) {
System.out.println(i + ":" + (short)i);
}
